本文共 3717 字,大约阅读时间需要 12 分钟。
前言
在微服务架构体系下,我们可以按照业务模块分层设计,单独部署,减轻了服务部署压力,也解耦了业务的耦合,避免了应用逐渐变成一个庞然怪物,从而可以轻松扩展,在某些服务出现故障时也不会影响其它服务的正常运行。总之,微服务在业务的高速发展中带给我们越来越多的优势,但是微服务并不是十全十美,因此不能盲目过度滥用,它有很多不足,而且会给系统带来一定的复杂度,其中伴随而来的分布式事务问题,是微服务架构体系下必然需要处理的一个痛点,也是业界一直关注的一个领域,因此也出现了诸如 CAP 和 BASE 等理论。
在今年年初,阿里开源了一个分布式事务中间件,起初起名为 Fescar,后改名为 Seata,在它开源之初,我就知道它肯定要火,因为这是一个解决痛点的开源项目,Seata 一开始就是冲着对业务无侵入与高性能方向走,这正是我们对解决分布式事务问题迫切的需求。
(想自学习编程的小伙伴请搜圈T社区]mhttp://www.ag-fquanti.co)(http://www.aiquanti.com)],更多行业相关资讯更有行业相关免费视频教程。完全免费哦!)
分布式事务解决的方案有哪些?
目前分布式事务解决的方案主要有对业务无入侵和有入侵的方案,无入侵方案主要有基于数据库 XA 协议的两段式提交(2PC)方案,它的优点是对业务代码无入侵,但是它的缺点也是很明显:必须要求数据库对 XA 协议的支持,且由于 XA 协议自身的特点,它会造成事务资源长时间得不到释放,锁定周期长,而且在应用层上面无法干预,因此它性能很差,它的存在相当于七伤拳那样“伤人七分,损己三分”,因此在互联网项目中并不是很流行这种解决方案。
为了这个弥补这种方案带来性能低的问题,大佬们又想出了很多种方案来解决,但这无一例外都需要通过在应用层做手脚,即入侵业务的方式,比如很出名的 TCC 方案,基于 TCC 也有很多成熟的框架,如 ByteTCC、tcc-transaction 等。以及基于可靠消息的最终一致性来实现,如 RocketMQ 的事务消息。
入侵代码的方案是基于现有情形“迫不得已”才推出的解决方案,实际上它们实现起来非常不优雅,一个事务的调用通常伴随而来的是对该事务接口增加一系列的反向操作,比如 TCC 三段式提交,提交逻辑必然伴随着回滚的逻辑,这样的代码会使得项目非常臃肿,维护成本高。
Seata 各模块之间的关系
针对上面所说的分布式事务解决方案的痛点,那很显然,我们理想的分布式事务解决方案肯定是性能要好而且要对业务无入侵,业务层上无需关心分布式事务机制的约束,Seata 正是往这个方向发展的,因此它非常值得期待,它将给我们的微服务架构带来质的提升。
那 Seata 是怎么做到的呢?下面说说它的各个模块之间的关系。
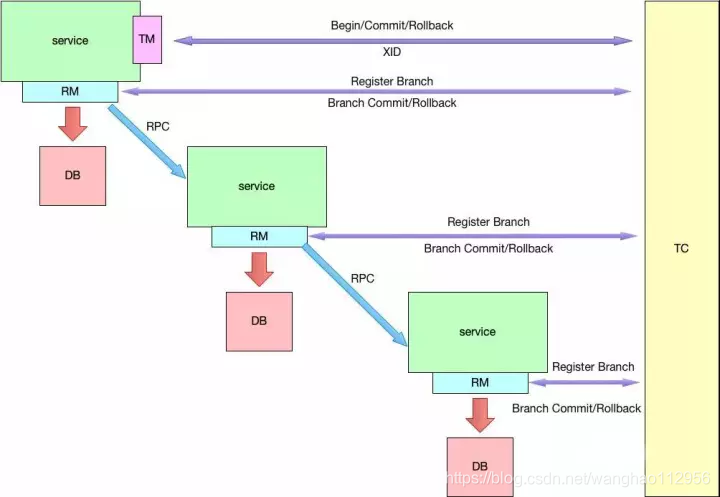
Seata 的设计思路是将一个分布式事务可以理解成一个全局事务,下面挂了若干个分支事务,而一个分支事务是一个满足 ACID 的本地事务,因此我们可以操作分布式事务像操作本地事务一样。Seata 内部定义了 3个模块来处理全局事务和分支事务的关系和处理过程,这三个组件分别是:
- •Transaction Coordinator (TC):事务协调器,维护全局事务的运行状态,负责协调并驱动全局事务的提交或回滚。
- •Transaction Manager ™:控制全局事务的边界,负责开启一个全局事务,并最终发起全局提交或全局回滚的决议。
- •Resource Manager (RM):控制分支事务,负责分支注册、状态汇报,并接收事务协调器的指令,驱动分支(本地)事务的提交和回滚。
 简要说说整个全局事务的执行步骤:
简要说说整个全局事务的执行步骤:
- TM 向 TC 申请开启一个全局事务,TC 创建全局事务后返回全局唯一的 XID,XID 会在全局事务的上下文中传播;
- RM 向 TC 注册分支事务,该分支事务归属于拥有相同 XID 的全局事务;
- TM 向 TC 发起全局提交或回滚;
- TC 调度 XID 下的分支事务完成提交或者回滚。
与 XA 方案有什么不同?
Seata 的事务提交方式跟 XA 协议的两段式提交在总体上来说基本是一致的,那它们之间有什么不同呢?
我们都知道 XA 协议它依赖的是数据库层面来保障事务的一致性,也即是说 XA 的各个分支事务是在数据库层面上驱动的,由于 XA 的各个分支事务需要有 XA 的驱动程序,一方面会导致数据库与 XA 驱动耦合,另一方面它会导致各个分支的事务资源锁定周期长,这也是它没有在互联网公司流行的重要因素。
基于 XA 协议以上的问题,Seata 另辟蹊径,既然在依赖数据库层会导致这么多问题,那我就从应用层做手脚,这还得从 Seata 的 RM 模块说起,前面也说过 RM 的主要作用了,其实 RM 在内部做了对数据库操作的代理层,如下:
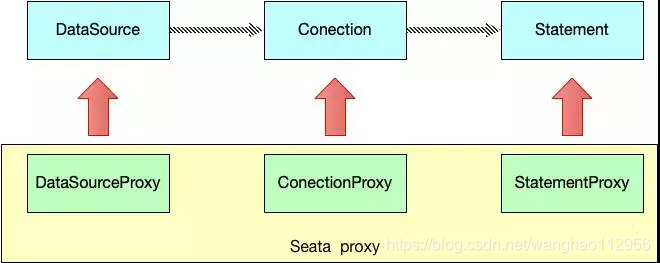 Seata 在数据源做了一层代理层,所以我们使用 Seata 时,我们使用的数据源实际上用的是 Seata 自带的数据源代理 DataSourceProxy,Seata 在这层代理中加入了很多逻辑,主要是解析 SQL,把业务数据在更新前后的数据镜像组织成回滚日志,并将 undo log 日志插入 undo_log 表中,保证每条更新数据的业务 sql 都有对应的回滚日志存在。
Seata 在数据源做了一层代理层,所以我们使用 Seata 时,我们使用的数据源实际上用的是 Seata 自带的数据源代理 DataSourceProxy,Seata 在这层代理中加入了很多逻辑,主要是解析 SQL,把业务数据在更新前后的数据镜像组织成回滚日志,并将 undo log 日志插入 undo_log 表中,保证每条更新数据的业务 sql 都有对应的回滚日志存在。 这样做的好处就是,本地事务执行完可以立即释放本地事务锁定的资源,然后向 TC 上报分支状态。当 TM 决议全局提交时,就不需要同步协调处理了,TC 会异步调度各个 RM 分支事务删除对应的 undo log 日志即可,这个步骤非常快速地可以完成;当 TM 决议全局回滚时,RM 收到 TC 发送的回滚请求,RM 通过 XID 找到对应的 undo log 回滚日志,然后执行回滚日志完成回滚操作。
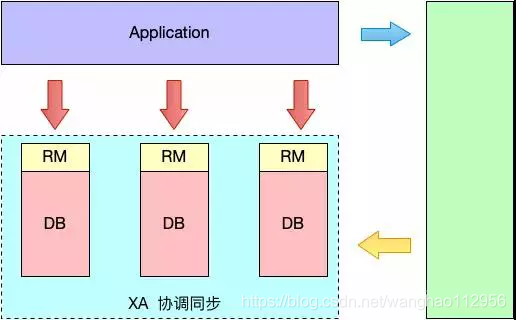
如上图所示,XA 方案的 RM 是放在数据库层的,它依赖了数据库的 XA 驱动程序。
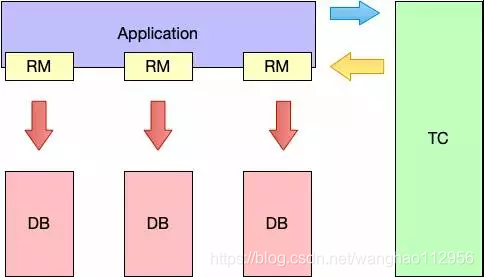 如上图所示,Seata 的 RM 实际上是已中间件的形式放在应用层,不用依赖数据库对协议的支持,完全剥离了分布式事务方案对数据库在协议支持上的要求。
如上图所示,Seata 的 RM 实际上是已中间件的形式放在应用层,不用依赖数据库对协议的支持,完全剥离了分布式事务方案对数据库在协议支持上的要求。 分支事务如何提交和回滚?
下面详细说说分支事务是如何提交和回滚的:
- •第一阶段:
分支事务利用 RM 模块中对 JDBC 数据源代理,加入了若干流程,对业务 SQL 进行解释,把业务数据在更新前后的数据镜像组织成回滚日志,并生成 undo log 日志,对全局事务锁的检查以及分支事务的注册等,利用本地事务 ACID 特性,将业务 SQL 和 undo log 写入同一个事物中一同提交到数据库中,保证业务 SQL 必定存在相应的回滚日志,最后对分支事务状态向 TC 进行上报。
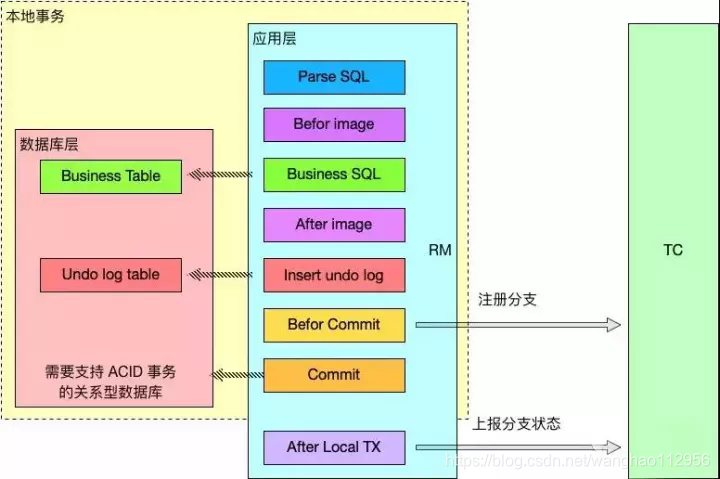
- •第二阶段: TM决议全局提交:
当 TM 决议提交时,就不需要同步协调处理了,TC 会异步调度各个 RM 分支事务删除对应的 undo log 日志即可,这个步骤非常快速地可以完成。这个机制对于性能提升非常关键,我们知道正常的业务运行过程中,事务执行的成功率是非常高的,因此可以直接在本地事务中提交,这步对于提升性能非常显著。
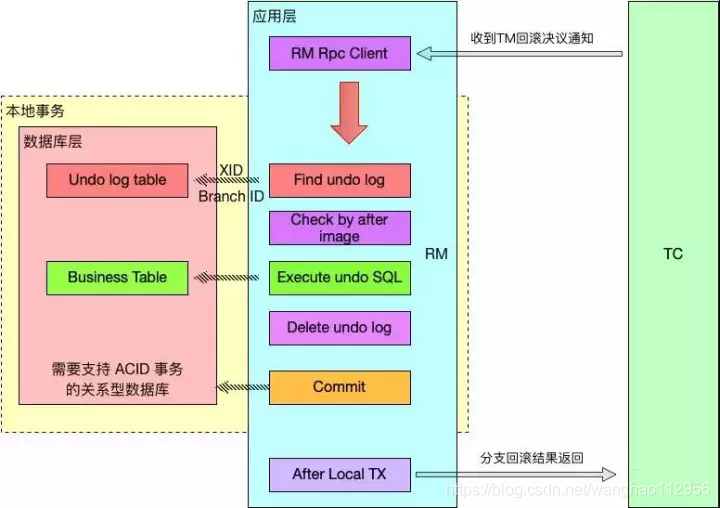
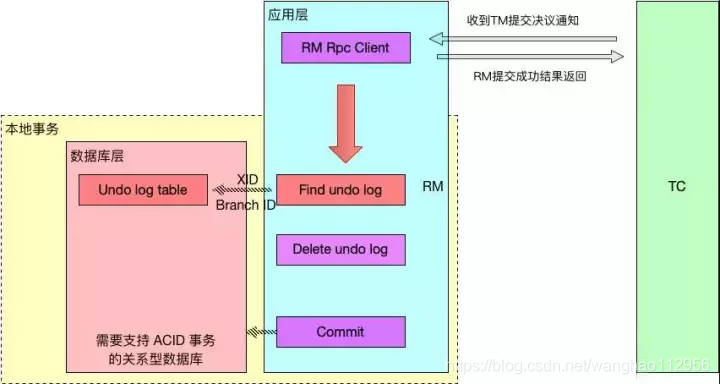 TM决议全局回滚:
TM决议全局回滚: 当 TM 决议回滚时,RM 收到 TC 发送的回滚请求,RM 通过 XID 找到对应的 undo log 回滚日志,然后利用本地事务 ACID 特性,执行回滚日志完成回滚操作并删除 undo log 日志,最后向 TC 进行回滚结果上报。
其它方案的补充
上面说的其实是 Seata 的默认模式,也叫 AT 模式,它是类似于 XA 方案的两段式提交方案,并且是对业务无侵入,但是这种机制依然是需要依赖数据库本地事务的 ACID 特性,有没有发现,我在上面的图中都强调了必须是支持 ACID 特性的关系型数据库,那么问题就来了,非关系型或者不支持 ACID 的数据库就无法使用 Seata 了,别慌,Seata 现阶段为我们准备了另外一种模式,叫 MT 模式,它是一种对业务有入侵的方案,提交回滚等操作需要我们自行定义,业务逻辑需要被分解为 Prepare/Commit/Rollback 3 部分,形成一个 MT 分支,加入全局事务,它存在的意义是为 Seata 触达更多的场景。
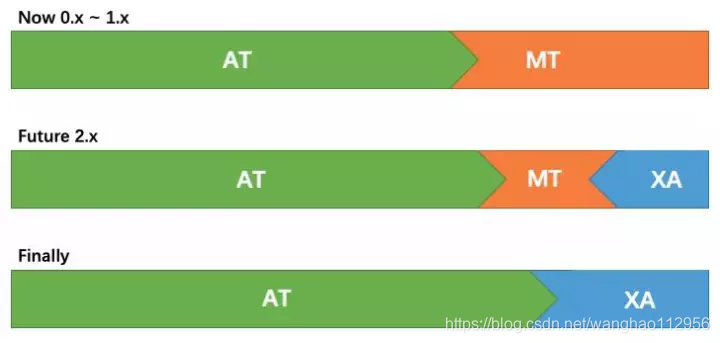 只不过,它不是 Seata “主打”的模式,它的存在仅仅作为补充的方案,从以上官方的发展远景就可以看出来,Seata 的目标是始终是对业务无入侵的方案。
只不过,它不是 Seata “主打”的模式,它的存在仅仅作为补充的方案,从以上官方的发展远景就可以看出来,Seata 的目标是始终是对业务无入侵的方案。 转载地址:http://fvbp.baihongyu.com/